4.3 Rysowanie wykresów funkcji y=f(x+a), y=f(x)+a, znając wykres y=f(x).
W wielu sytuacjach życiowych mamy do czynienia z funkcjami, np. w statystyce gdy podana jest tabela z danymi statystycznymi, to określa ona pewne przyporządkowanie, wg którego każdemu elementowi jednego zbioru odpowiada element należący do drugiego zbioru.
Definicja
- argument funkcji
lub
- wartość funkcji
- dziedzina funkcji
- przeciwdziedzina funkcji
- zbiór wartości funkcji
Zapisujemy funkcje małymi literami
- funkcja
odwzorowujaca zbiór
w zbiór
- funkcja
odwzorowuje zbiór
na zbiór
- zapis funkcji używany przy wykresie

Dane jest odwzorowanie: każdej liczbie naturalnej dodatniej przyporządkowujemy jej kwadrat. Podaj dziedzinę i zbiór wartości oraz zapisz tę funkcję.

Zauważ, że podane zdanie spełnia warunki definicji funkcji, gdyż dowolnej liczbie naturalnej odpowiada dokładnie jedna liczba, która jest jej kwadratem. Użyty został zapis słowny funkcji.
Rozwiązanie.
- liczba naturalna,
- wartość funkcji dla argumentu
Zapisujemy funkcję w postaci wzoru
Jest to ciąg liczbowy, który zapisujemy również
Dziedzina
Przeciwdziedzina
Zbiór wartości
Często funkcję zapisujemy w postaci co praktycznie oznacza zbiór wszystkich uporządkowanych par
gdzie
jest wartością funkcji
dla argumentu
Zbiór takich par tworzy w układzie współrzędnych wykres funkcji

Zauważ, że w podanym przykładzie wykres będzie nieskończonym zbiorem punktów zaznaczonych w prostokątnym układzie współrzędnych leżących na paraboli w prawej półpłaszczyżnie o współrzędnych
Przekształcanie wykresów funkcji
Znając wykres funkcji mamy za zadanie narysowanie wykresów, które uzyskujemy przy użyciu pewnych przekształceń geometrycznych.
Przesunięcia punktów wzdłuż osi układu współrzędnych
W wyniku przesunięcia punktu w układzie współrzędnych uzyskujemy punkt
który nazywamy obrazem punktu

Przesuńmy wzdłuż osi punkty
o jednostki
o jednostki
Jakie obrazy otrzymamy?
Rozwiązanie.
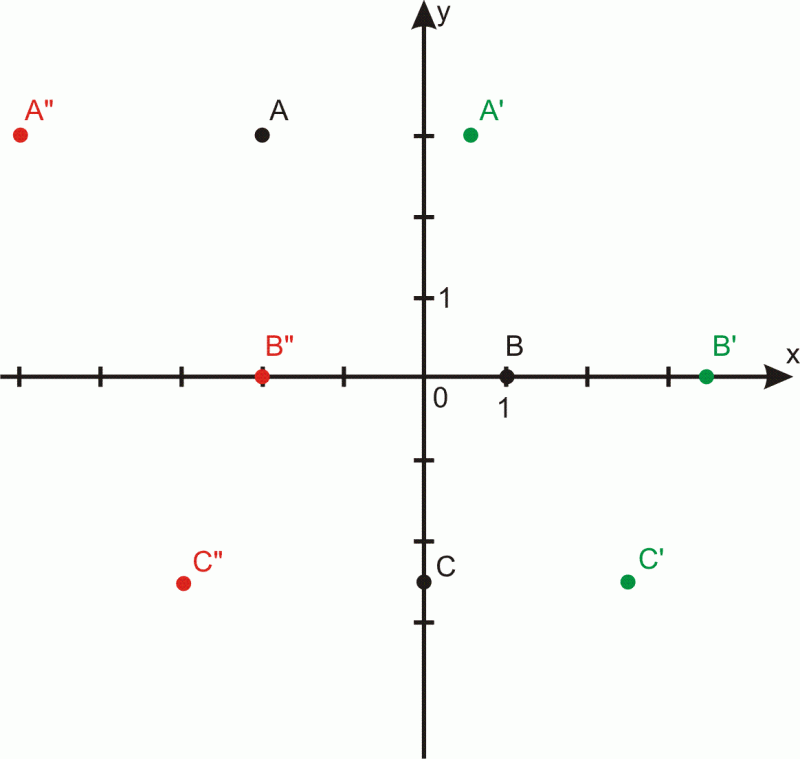
Przesunięcie o jednostki wzdłuż osi
oznacza zaznaczenie punktu na prawo od danego punktu w linii równoległej do osi
Obrazami punktów w tym przekształceniu są
Odczytujemy współrzędne
Uzyskane punkty mają drugie współrzędne (rzędne) takie same, a pierwsze (odcięte) zwiększone o
Przesunięcie o jednostki wzdłuż osi
oznacza zaznaczenie punktu na lewo od danego punktu w linii równoległej do osi
Obrazami punktów w tym przekształceniu są
Odczytujemy współrzędne
Uzyskane punkty mają drugie współrzędne (rzędne) takie same, a pierwsze (odcięte) zmniejszone o

Jeśli przesuwamy w prawo. Jeśli
przesuwamy w lewo.

Znane są punkty
Podaj regułę, wg której po przesunięciu wzdłuż osi uzyskamy z powrotem punkty
Skorzystaj z rysunku podanego w przykładzie powyżej.
Rozwiązanie.
Korzystając z rysunku zauważamy, że odcięte punktów należy zmniejszyć o
aby uzyskać punkty


Przesuńmy wzdłuż osi
o
o
Jakie obrazy otrzymamy?
Rozwiązanie.
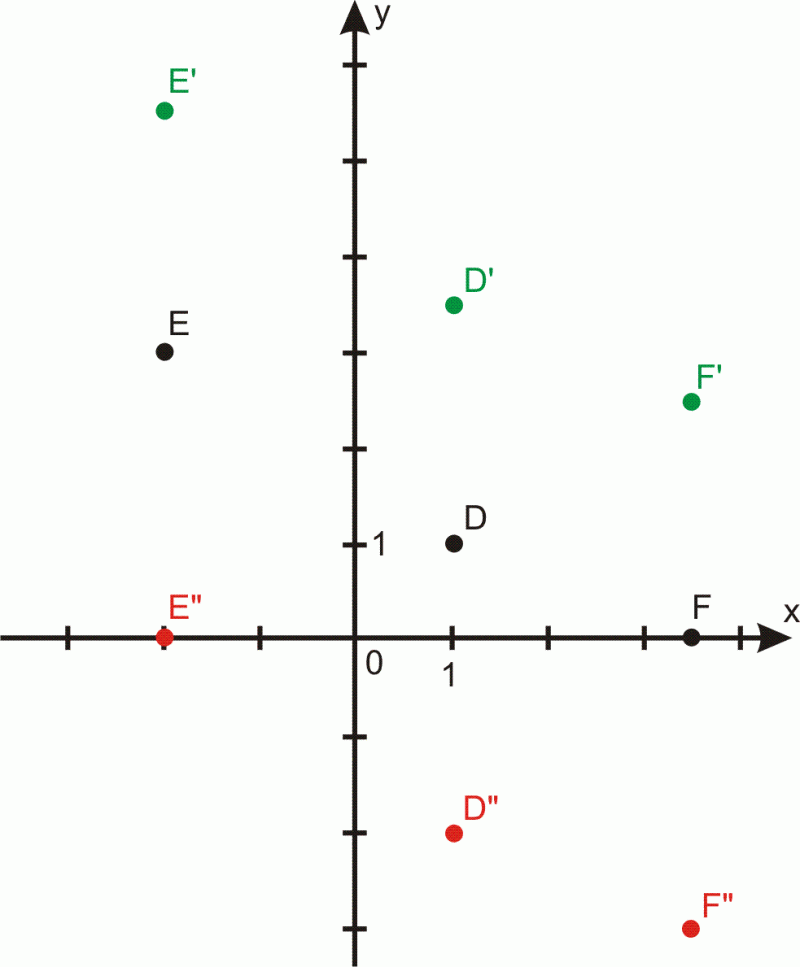
Przesunięcie o jednostki wzdłuż osi
oznacza przeniesienie punktu do góry względem danego punktu w linii równoległej do osi
Obrazami punktów w tym przekształceniu są
Odczytujemy współrzędne
Uzyskane punkty mają odcięte takie same, a rzędne zwiększone o
Przesunięcie o jednostki wzdłuż osi
oznacza przeniesienie punktu do dołu względem danego punktu w linii równoległej do osi
Punkty w tym przekształceniu zostały przesunięte do
Odczytujemy współrzędne
Uzyskane punkty mają odcięte takie same, a rzędne zmniejszone o

Po przesunięciu punktu
Jeśli przesuwamy do góry. Jeśli
przesuwamy do dołu.

Znane są punkty
Podaj regułę, wg której po przesunięciu wzdłuż osi uzyskamy z powrotem punkty
Skorzystaj z rysunku do poprzedniego przykładu.
Rozwiązanie.
Korzystając z rysunku zauważamy, że rzędne punktów należy zmniejszyć o
aby uzyskać punkty

Przesunięcia wykresów funkcji wzdłuż osi układu współrzędnych

Dany jest na rysunku wykres funkcji i dwa wykresy
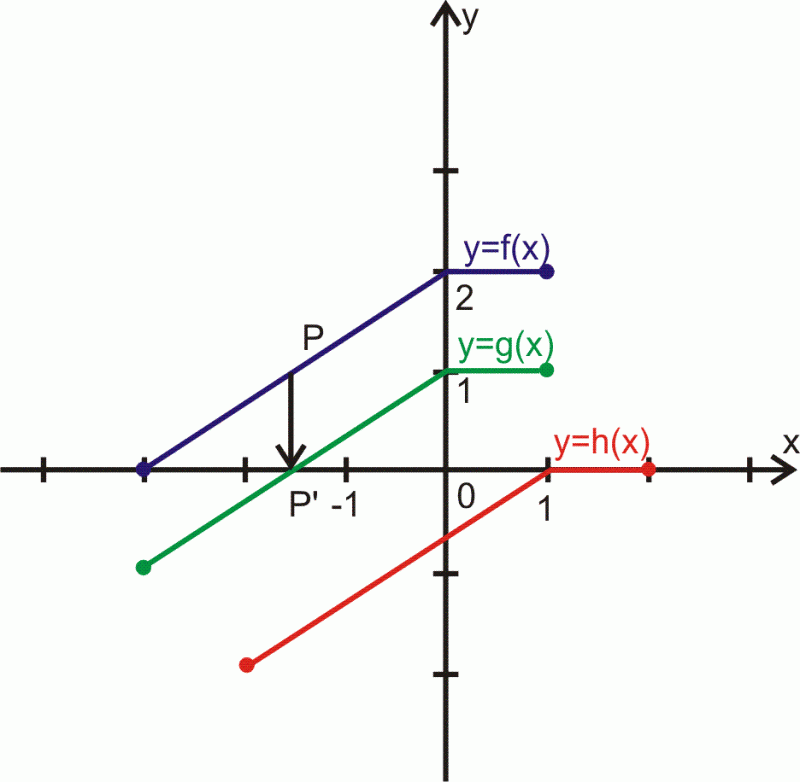
Który z wykresów funkcji czy
jest uzyskany z przesunięcia wykresu funkcji
wzdłuż osi
a który wzdłuż osi
i o ile jednostek?
Rozwiązanie.
Wykresy funkcji są figurami przystającymi, każdy jest łamaną zbudowaną z dwóch odcinków.
Wykresy dwóch funkcji wskazują, że funkcje mają taką samą dziedzinę, jeden z nich
jest krzywą uzyskaną z przesunięcia do dołu, wzdłuż osi
o
wykresu
Każdy punkt
wykresu funkcji
ma rzędną
zmniejszoną o
w stosunku do rzędnej
odpowiedniego punktu
wykresu funkcji
Wniosek 1
Dla funkcji uzyskanej z przesunięcia do dołu o
wzdłuż osi
można zauważyć, że wartości funkcji
są mniejsze o
od wartości funkcji
dla tych samych argumentów
Zatem dla
Krzywą można uzyskać z przesunięcia wykresu funkcji
w pierwszym etapie wzdłuż osi
do dołu o
a w drugim etapie wzdłuż osi
o
w prawo.
I etap
Po przesunięciu do dołu wzdłuż osi z wykresu funkcji
uzyskamy wykres funkcji
dla
II etap
Zaznaczmy wykresy funkcji na osobnym rysunku.
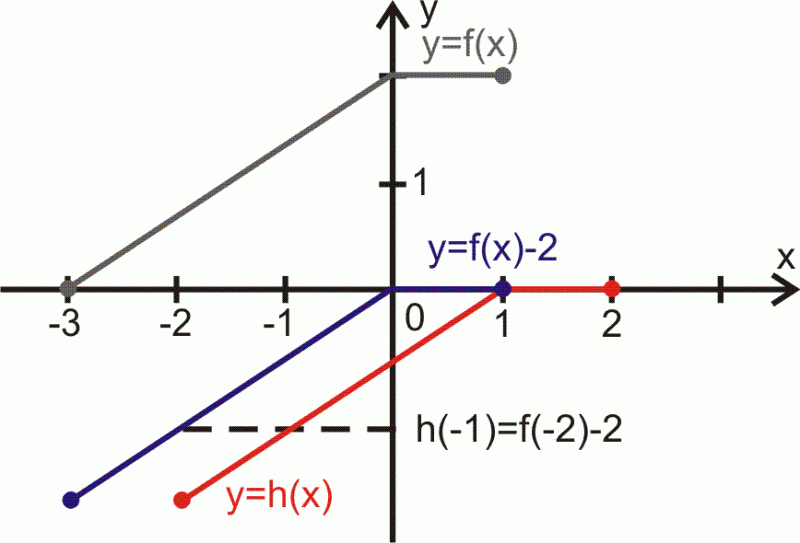
Wniosek 2
Zauważmy, że obie funkcje mają te same wartości funkcji dla argumentów różniących się o
I tak
Zatem można napisać wzór na w zależności od

Zauważ, że efekt uzyskania wykresu funkcji w wyniku przesunięć wykresu funkcji
uzyskamy taki sam jeśli w pierwszym etapie krzywą
przesuniemy w prawo wzdłuż osi
o
i w drugim etapie uzyskany wykres przesuniemy o
wzdłuż osi

Z wykresów funkcji podanych na rysunku wybierz ten, który można otrzymać z przesunięcia wykresu
wzdłuż osi
układu współrzędnych .
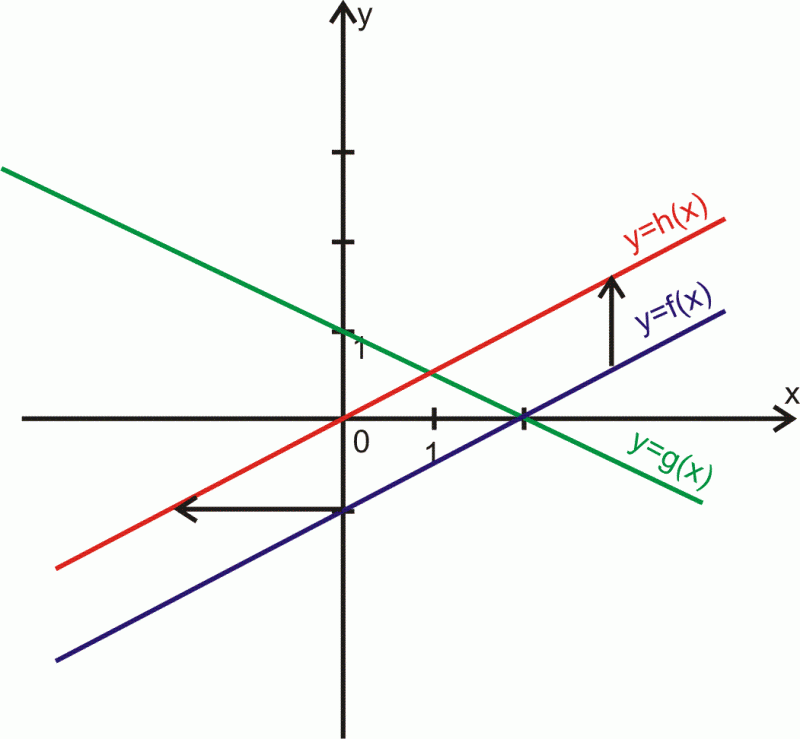
Rozwiązanie.
Każdy wykres na rysunku jest prostą, ale tylko dwa są do siebie równoległe.
Z rysunku można zauważyć, że każdy punkt wykresu można przesunąć o
do góry wzdłuż osi
i otrzymać prostą
Proste te są do siebie równoległe.
Można zapisać, że z przesunięcia o wzdłuż osi
Prostej nie uzyskamy przesuwając wykres funkcji
wzdłuż osi
lub wzdłuż osi
Potrzebujemy do tego wykorzystać inne przekształcenie geometryczne np. obrót.

Zauważ, że prostą można uzyskać z przesunięcia wykresu
w lewo wzdłuż osi
o
Zatem
można zapisać w postaci
Przedstawienie funkcji w postaci dwóch związków z funkcją
sprawdzimy na podstawie wzoru funkcji
Otóż
Wtedy daje wzór
czyli
Podobnie daje wzór
czyli

Jakiego przekształcenia dokonać, aby z wykresu funkcji otrzymać wykresy funkcji
z podanego rysunku?
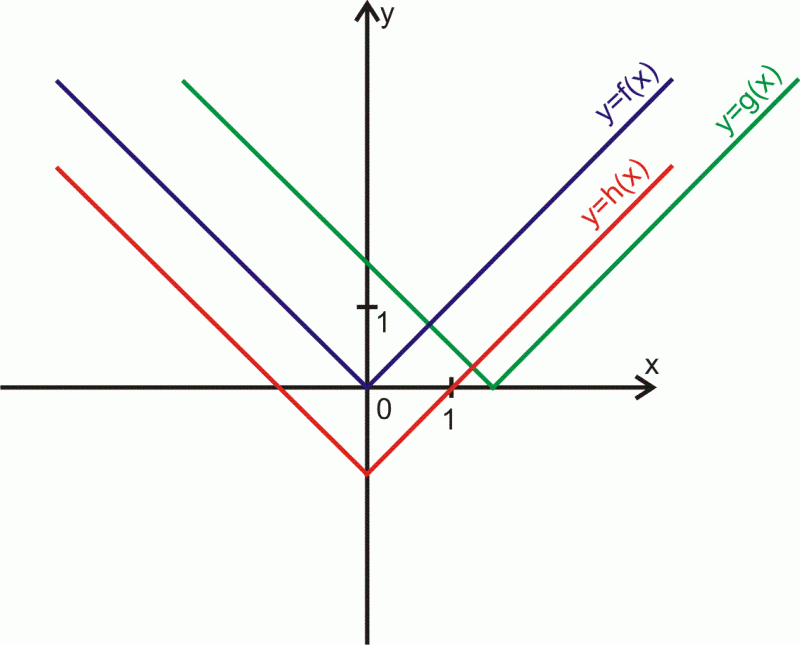
Podaj wzory funkcji przy pomocy
Ustal miejsca zerowe funkcji
i podaj funkcję, dla której miejsce zerowe możesz odczytać znając miejsce zerowe funkcji

Dla funkcji liczba
jest miejscem zerowym, gdy
Np. dla funkcji liczba
jest miejscem zerowym, bo
Rozwiązanie.
Na rysunku wykres funkcji leży na prawo od wykresu funkcji
a wykres funkcji
poniżej wykresu
Wszystkie wykresy są figurami przystającymi.
Wykres funkcji jest otrzymany z przesunięcia wykresu funkcji
wzdłuż osi
o
jednostki w prawo, zatem wzór funkcji
zapisany przy pomocy funkcji
ma postać
Wykres funkcji jest otrzymany z przesunięcia wykresu funkcji
wzdłuż osi
o
jednostkę do dołu, zatem wzór funkcji
zapisany przy pomocy funkcji
ma postać
Ustalamy miejsca zerowe funkcji
-
Dla funkcji
-
Dla funkcji
I warto zauważyć, że
oznacza wobec
równanie
Ponieważ funkcja przyjmuje wartość
dla argumentu
to
Zatem miejsce zerowe funkcji można odczytać znając miejsce zerowe funkcji
której wykres został przesunięty wzdłuż osi
do położenia wykresu funkcji
Wniosek
Jeżeli dane są funkcje oraz
jest miejscem zerowym funkcji
to miejsce zerowe funkcji
jest równe
-
Dla funkcji
Z rysunku odczytujemy, że miejscami zerowymi funkcji są liczby
Ze wzoru zauważamy, odczytane miejsca zerowe jako rozwiązania równania
są rozwiązaniami równania
a nie


Odczytaj z rysunku przesunięcie względem osi układu współrzędnych
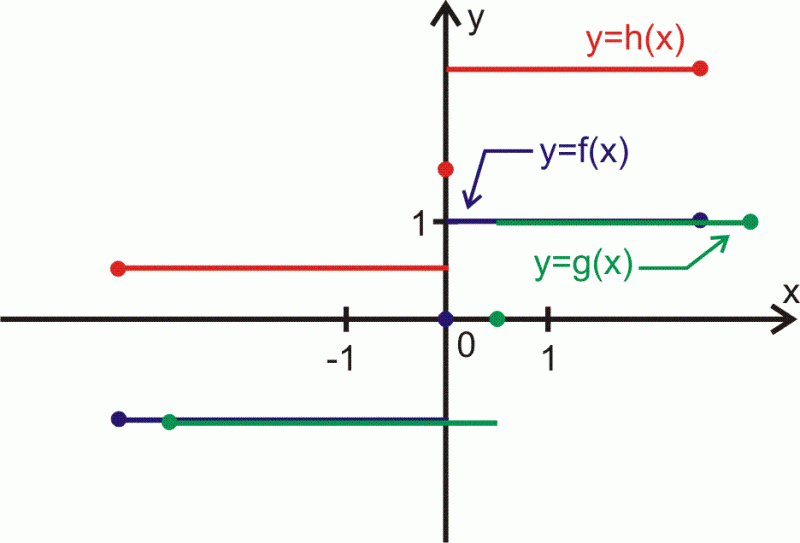
wykresu funkcji tak, aby otrzymać wykres funkcji
i podaj wzór na
w zależności od
wykresu funkcji tak, aby otrzymać wykres funkcji
i podaj wzór na
w zależności od
wykresu funkcji tak, aby otrzymać wykres funkcji
i podaj wzór na
w zależności od

Jeżeli wykres funkcji przesuniemy do góry wzdłuż osi
o
jednostki
otrzymujemy przesunięcie:
punktu należącego do wykresu funkcji
do punktu
należącego do wykresu
odcinek o końcach w punktach przesuwamy tak, że pokryje się z odcinkiem o końcach
odcinek o końcach przejdzie na odcinek o końcach
Zatem z wykresu funkcji otrzymamy wykres funkcji
po przesunięciu wzdłuż osi
o
do góry.
-
Wzór funkcji
Wykres funkcji przesuwamy wzdłuż osi
w lewo tak, aby np. punkt
przekształcić na punkt
Przesunięcie jest więc wzdłuż osi
o
-
Wzór funkcji
przy pomocy funkcji
Aby z wykresu funkcji otrzymać wykres funkcji
można go w pierwszym kroku przesunąć o
jednostki do góry wzdłuż osi
a w drugim kroku przesunąć o
jednostki w lewo wzdłuż osi
I krok
Przesunięcie wykresu funkcji o
wzdłuż osi
pozwala napisać wzór uzyskanej funkcji, otrzymujemy
II krok
Po przesunięciu wzdłuż osi o
punkt
wykresu
przechodzi na punkt
wobec tego trzeba dokonać następnego przesunięcia o
wzdłuż osi
Otrzymujemy wtedy wykres funkcji z wykresu
-
Wzór funkcji
Odp.

Dana jest funkcja w postaci tabeli
|
|
|
|
|
|
|
|
|
|
|
|
|
|
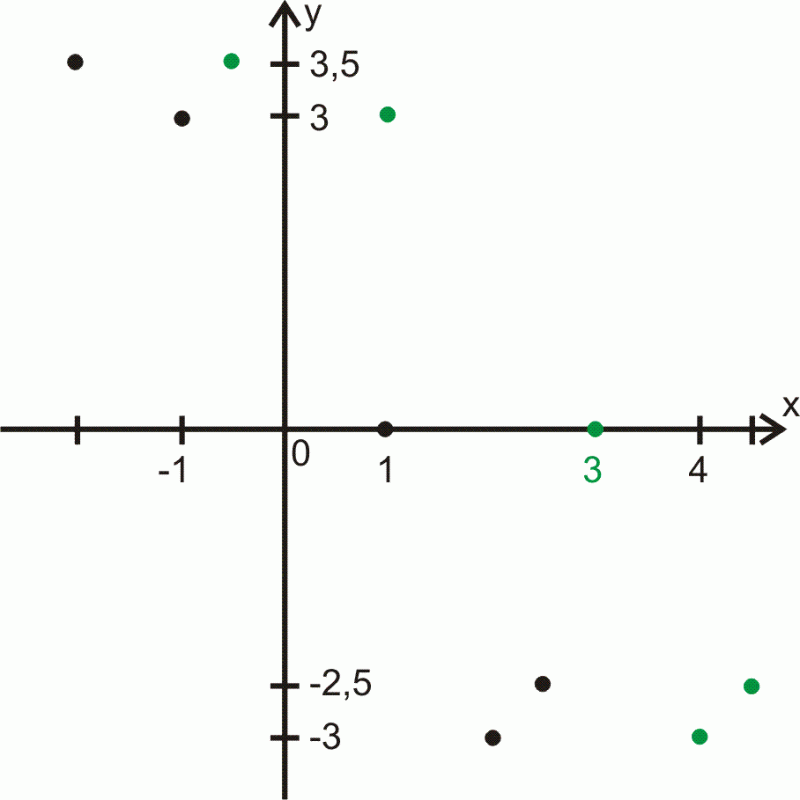
Przesuń wykres funkcji wzdłuż osi układu współrzędnych tak, aby miejsce zerowe funkcji po przesunięciu było
Zbuduj tabelę uzyskanej funkcji.


Przesunięcie funkcji wzdłuż osi zmienia argumenty funkcji zachowując wartości funkcji, a wzdłuż osi
zachowuje argumenty zmieniając wartości funkcji.
Wobec tego należy przesunąć funkcję wzdłuż osi
Istnieje liczba a taka, że funkcja ma miejsce zerowe
Zatem
Miejsce zerowe funkcji wobec tabeli, jest jedno, więc
Funkcja po przesunięciu jest postaci
Budujemy tabelę
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Odp.
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Podaj jaką postać funkcji otrzymasz po przesunięciu wykresu funkcji
a) o wzdłuż osi
b) o wzdłuż osi
i następnie o
jednostki w prawo wzdłuż osi
c) w lewo o jednostki wzdłuż osi

A wtedy po przesunięciu otrzymujemy wykres funkcji
Przesuwamy wykres funkcji o
wzdłuż osi
i następnie o
jednostki w prawo wzdłuż osi
Dokonujemy przesunięcia o
wzdłuż osi
otrzymujemy wykres funkcji
Przesuwamy otrzymany wykres o jednostki w prawo wzdłuż osi
i otrzymujemy wykres funkcji
Przesunięcie w lewo o jednostki wzdłuż osi
daje wzór funkcji w postaci
Odp. a) b)
c)

Podaj przesunięcie wykresu funkcji takie, aby otrzymać wykres funkcji
a)
b)
c)

Aby z otrzymać
trzeba wykres funkcji
przesunąć o
jednostki do dołu wzdłuż osi
Aby z otrzymać
trzeba wykres funkcji
przesunąć o
jednostki w lewo wzdłuż osi
czyli o
wzdłuż osi
a następnie o
do dołu wzdłuż osi
Odp. a) O jednostki w prawo wzdłuż osi
b) O
jednostki do dołu wzdłuż osi
c) O
jednostki w lewo wzdłuż osi
i o
do dołu wzdłuż osi


Wykonaj w kolejności
Krok 1.
Punkty przesuń odpowiednio:
do położenia
czyli
gdzie
oraz podaj jakich przesunięć dokonałeś.
Krok 2.
Połącz uzyskane punkty oznaczając je przez aby uzyskać figurę geometryczną
Przesuń ją o najpierw wzdłuż osi
a następnie wzdłuż osi
Oznacz figurę po przesunięciu używając zapisów
Podaj długości odcinków

Krok 2. Ze współrzędnych punktów po przekształceniu odczytaj długości potrzebnych odcinków.
Rozwiązanie.
Krok 1.
Dane punkty
spełniają warunki stąd punkt
przesuwamy wzdłuż osi
a punkt
przesuwamy wzdłuż osi
i to w pierwszym przypadku o
do dołu, a w drugim o
jednostki w prawo, natomiast punkt
trzeba przesunąć wzdłuż osi
o
jednostki do góry.
Krok 2.
Sporządzamy rysunek i nanosimy oznaczenia
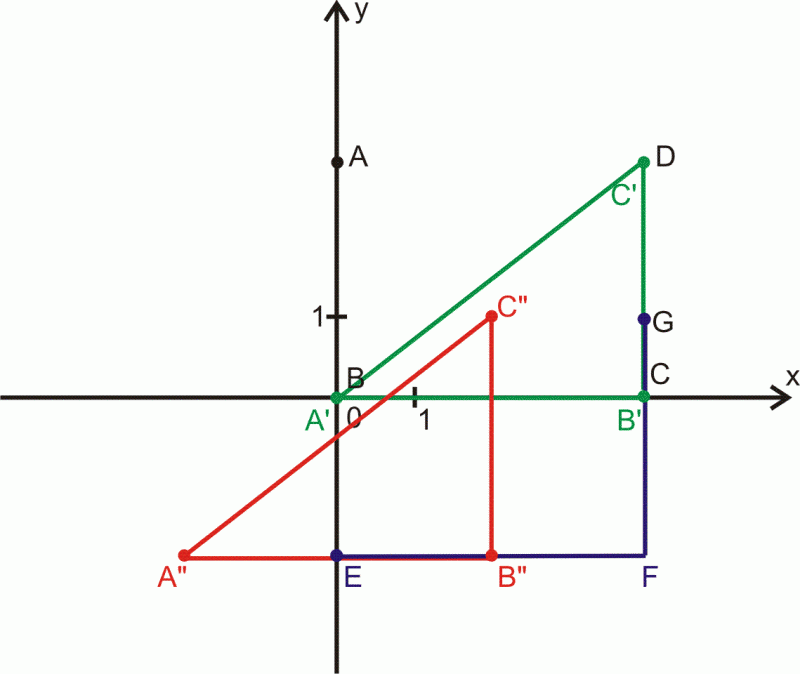
Otrzymaną figurą po połączeniu punktów jest trójkąt prostokątny i po przesunięciu otrzymujemy trójkąt przystający do niego o wierzchołkach

Ustalamy długości odcinków, które są przeciwprostokątnymi odpowiednich trójkątów prostokątnych
- z trójkąta
Podobnie
- odpowiednio z trójkątów
Odp. Krok 1. - wzdłuż osi
o
-wzdłuż osi
o
- wzdłuż osi
o
Krok 2. Długości odcinków są równe

Na rysunku dane są wykresy
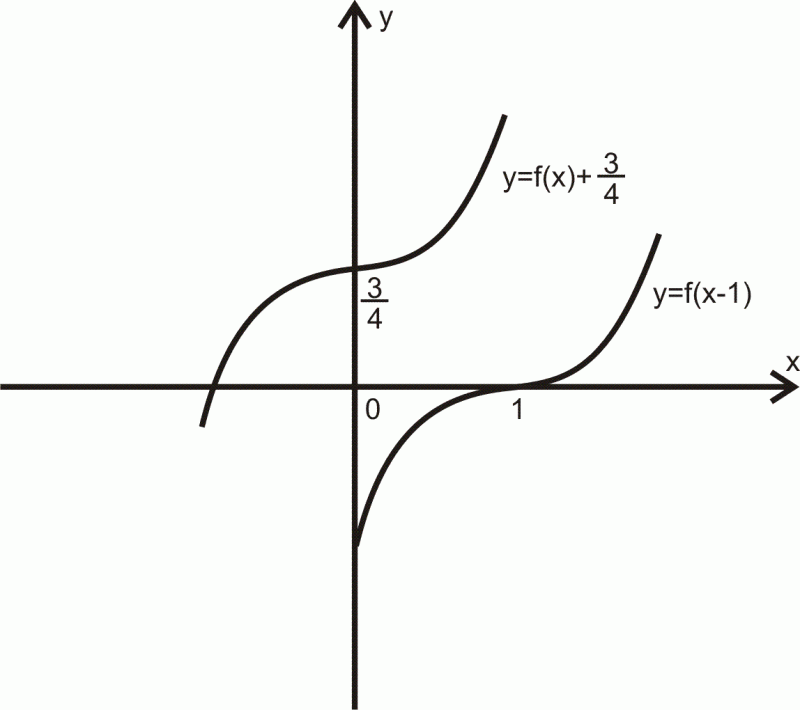
Podaj miejsce zerowe funkcji i punkt przecięcia funkcji
z osią

Rozwiązanie.
Oznaczenie
Z rysunku odczytujemy wartość funkcji dla argumentu
i miejsce zerowe funkcji
Zatem podstawiając do wzorów funkcji mamy
Wykres funkcji przecina oś
w punkcie
a funkcja
ma miejsce zerowe
Odp. - miejsce zerowe;
- punkt przecięcia z osią

Dana jest funkcja której wykres zwany parabolą przedstawiono na rysunku.
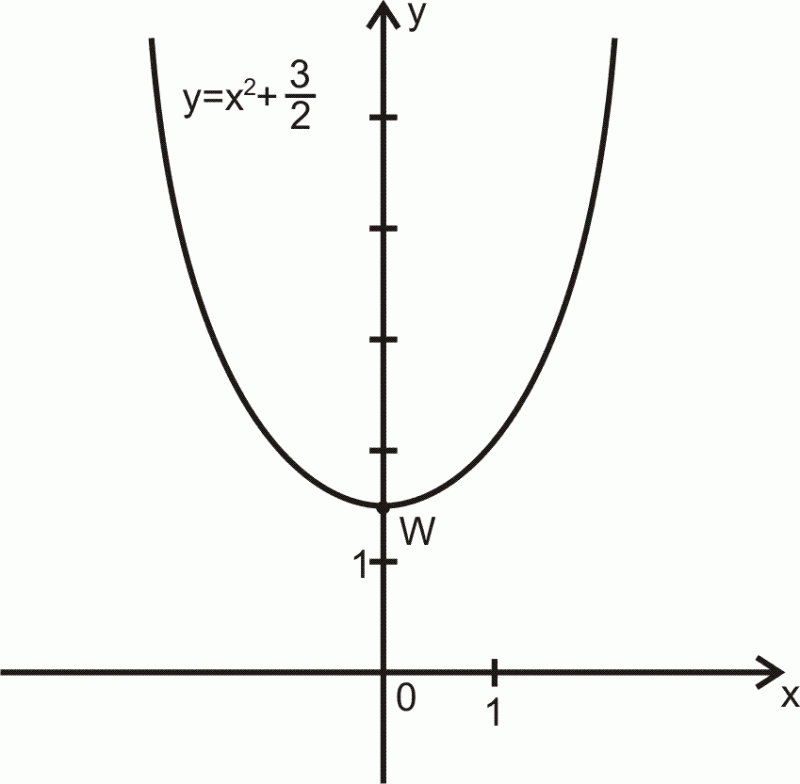
Punkt przesuwamy o
jednostki w prawo wzdłuż osi
Podaj: wzór funkcji po tym samym przesunięciu oraz argument w którym funkcja przyjmuje wartość najmniejszą.

Rozwiązanie.
Wobec reguły obraz punktu
uzyskany w przesunięciu wzdłuż osi
o
jednostek ma współrzędne
co dla daje
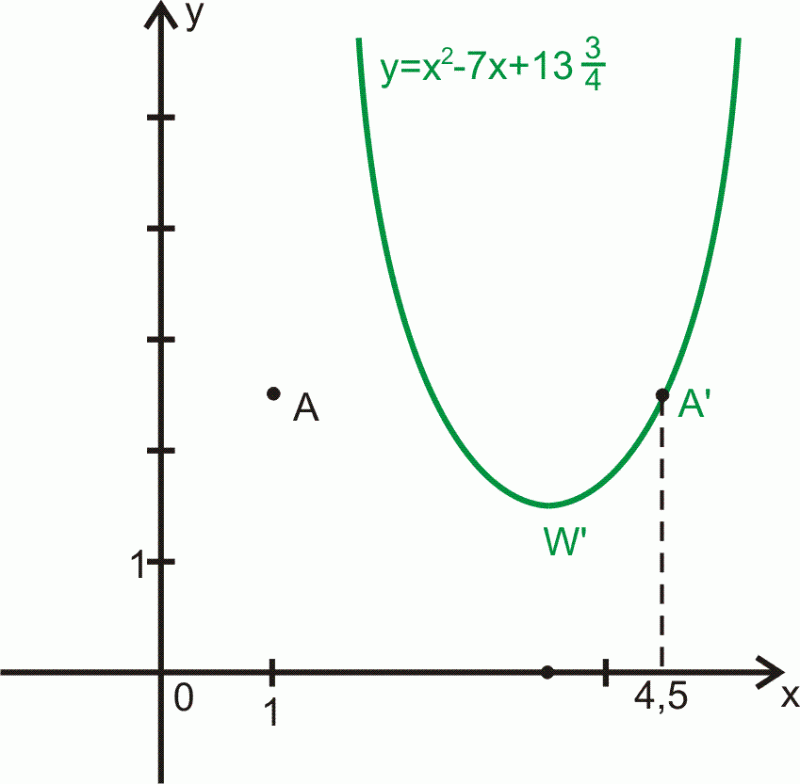
Wzór funkcji po przesunięciu jest postaci
Punkt po przesunięciu ma obraz
Tak więc argument, dla którego wartość funkcji jest najmniejsza jest
Odp.

Punkty o odciętej
o odciętej
należą do prostej, która jest wykresem funkcji
Prostą przesunięto wzdłuż osi
tak aby po przesunięciu przechodziła przez punkt
a obrazy punktów
oznaczono
Oblicz długości odcinków
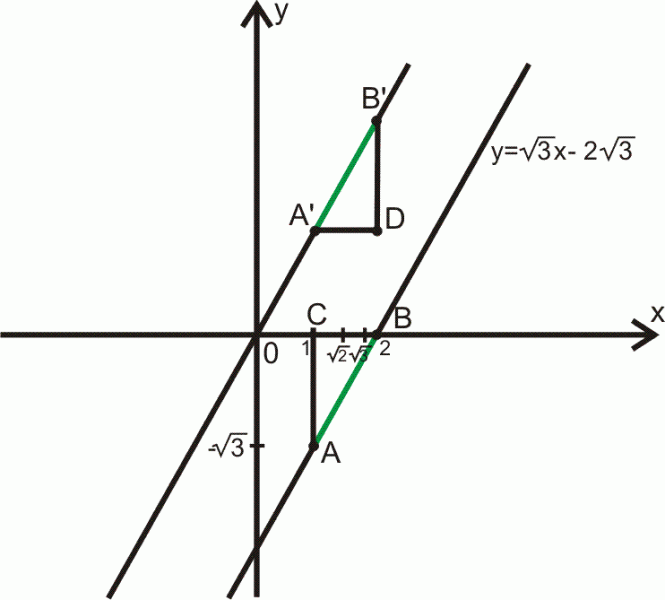

Rozwiązanie.
Obliczamy rzędne punktów
Punkt ma odciętą równą
i rzędną równą
Zatem z trójkąta prostokątnego
Po przesunięciu proste są równoległe, a punkt jest obrazem punktu wspólnego prostej
i osi
czyli punktu
Zatem wykres funkcji przesunięto o
w górę wzdłuż osi
Obliczamy rzędne punktów
Przy przesunięciu wzdłuż osi odcięte punktów się zachowują, zatem
Współrzędne wierzchołka trójkąta prostokątnego
obliczamy podobnie jak dla punktu
Z trójkąta
Odp.

![]()

Z podanego na rysunku wykresu funkcji po przesunięciu wzdłuż osi
i osi
otrzymano wykres funkcji
Podaj przesunięcia wzdłuż obu osi aby z jednego wykresu otrzymać drugi.
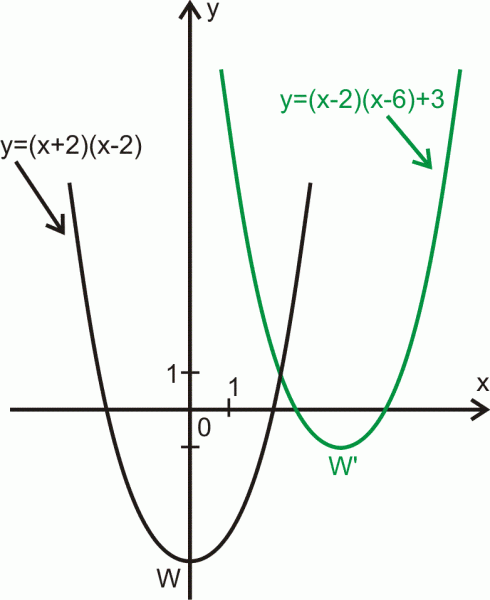

Ustalimy przesunięcie wierzchołka do
Odpowiednie współrzędne tych punktów nie są takie same, a więc trzeba dokonać przesunięcia wzdłuż obu osi.
Aby z punktu otrzymać punkt
trzeba przesunąć dany punkt wzdłuż osi
do góry i wzdłuż osi
w prawo.
Krok 1.
Przesuwamy punkt do góry o
wzdłuż osi
i otrzymujemy punkt
Z wykresu funkcji
otrzymamy wykres funkcji
Krok 2.
Otrzymany punkt ma taką samą drugą współrzędną jak punkt
Wobec tego przesuwamy punkt
o
jednostki w prawo wzdłuż osi
Z wykresu funkcji
otrzymamy przy tym przesunięciu
czyli
Dokonując przesunięcia wykresu wzdłuż osi
o
a następnie wzdłuż
osi o
otrzymujemy wykres funkcji
Przesuwamy wykres do położenia
Wystarczy oczywiście przesunąć o jednostki w lewo wzłuż osi
i o
jednostki do dołu wzdłuż osi

Odp. Wykres
Wykres
Do góry ∧
- Szkoła Podstawowa (4-6)
- 1. Liczby naturalne
- 2. Liczby całkowite
- 3. Ułamki zwykłe i dziesiętne
- 4. Działania na ułamkach zwykłych i dziesiętnych
- 5. Elementy algebry
- 6. Proste i odcinki
- 7. Kąty
- 8. Wielokąty, koła i okręgi
- 9. Bryły
- 9.1 Figury przestrzenne. Bryły....
- 9.2 Siatki brył: graniastosłup ...
- 9.3 Pole i objętość ...
- 9.4 Zamiana jednostek długości....
- 9.4.2 Obwody wielokątów z ...
- 9.4.3 Podstawowe jednostki pola. ...
- 9.4.4 Pola wielokątów z ...
- 9.4.5 Poznawanie jednostek ...
- 9.4.6 Miary kątów wielokąta. ...
- Klasówki (9)
- 10. Obliczenia praktyczne
- 11. Elementy statystyki opisowej
- 12. Zadania tekstowe
- Klasy IV-VI reforma 2017...
- Wzory
- Nauczyciele
- Arkusze maturalne CKE matematyka
- Arkusze maturalne próbne MegaMatma z matematyki
- Wszystkie klasówki (200)
- Szkoła Podstawowa (7-8)
- 1. Liczby wymierne dodatnie
- 1.1 Liczby w systemie rzymskim....
- 1.2 Ułamki zwykłe, rozszerzanie ...
- 1.2.2 Liczby wymierne....
- 1.2.3 Dodawanie i odejmowanie ...
- 1.2.4 Ułamki dziesiętne....
- 1.2.5 Mnożenie i dzielenie liczb ...
- 1.3 Działania na liczbach ...
- 1.4 Działania na ułamkach ...
- 1.5 Zamiana ułamków zwykłych ...
- 1.6 Zamiana ułamków ...
- 1.7 (>R) Zamiana liczby ...
- 1.8 Zaokrąglanie rozwinięć ...
- 1.9 Wartości wyrażeń ...
- 1.10 Zastosowanie zamiany ...
- Klasówki (24)
- 2. Liczby wymierne dowolne
- 3. Potęgi
- 4. Pierwiastki
- 5. Procenty
- 6. Wyrażenia algebraiczne
- 6.1 Zapisywanie i czytanie ...
- 6.2 Wartość liczbowa wyrażenia ...
- 6.3 Redukcja wyrazów podobnych. ...
- 6.4 Dodawanie i odejmowanie sum ...
- 6.5 Mnożenie sum algebraicznych ...
- 6.6 Kwadrat sumy wyrażeń ...
- 6.7 Różnica kwadratów ...
- 6.8 Wyłączanie wspólnego ...
- 6.9 Wyznaczanie podanej ...
- 6.10 (>R) Rozkład wyrażeń ...
- Klasówki (22)
- 7. Równania
- 8. Nierówności
- 9. Wykresy funkcji
- 10. Statystyka
- 10P Prawdopodobieństwo
- 11. Figury płaskie
- 11.1 Kąty utworzone przez prostą ...
- 11.2 Położenie prostej i ...
- 11.3 Wykorzystanie faktu, że ...
- 11.4 (>R) Położenie dwóch ...
- 11.5 Kąty środkowe. (>R) ...
- 11.6 Obliczanie długości okręgu....
- 11.7 Obliczanie długości łuku ...
- 11.8 Obliczanie pola koła....
- 11.9 Obliczanie pola pierścienia ...
- 11.10 Obliczanie pola wycinka ...
- 11.11 Twierdzenie Pitagorasa. ...
- 11.12 Kąty i przekątne w ...
- 11.12.2 Kąty i przekątne w ...
- 11.13 Obliczanie pól i obwodów ...
- 11.14 Zamiana jednostek pola....
- 11.15 (>R) Proporcje i reguła ...
- 11.16 (>R) Twierdzenie Talesa....
- 11.17 Powiększenie lub ...
- 11.18 Stosunek pól wielokątów ...
- 11.19 Wielokąty podobne i ...
- 11.20 Cechy przystawania ...
- 11.21 (>R) Cechy podobieństwa ...
- 11.22 Cechy podobieństwa ...
- 11.23 Figury symetryczne względem ...
- 11.24 Figury symetryczne względem ...
- 11.25 Figury, które mają oś ...
- 11.26 Figury, które mają środek ...
- 11.27 Symetralna odcinka, ...
- 11.28 Dwusieczna kąta, konstrukcja ...
- 11.29 Konstrukcje kątów 60°, ...
- 11.30 Okrąg opisany na ...
- 11.31 Okrąg wpisany w trójkąt, ...
- 11.32 Wielokąty foremne ...
- 11.33 (>R)Symetria w układzie ...
- Klasówki (66)
- 12. Bryły
- 12.1 Graniastosłup prawidłowy....
- 12.2 Ostrosłup prawidłowy....
- 12.3 Obliczanie pól powierzchni i ...
- 12.4 Obliczanie pól powierzchni ...
- 12.5 Obliczanie pól powierzchni i ...
- 12.6 Obliczanie pól powierzchni i ...
- 12.7 Obliczanie pól powierzchni i ...
- 12.8 Zamiana jednostek objętości....
- 12.9 (>R)Przekroje brył....
- Klasówki (18)
- Klasy VII-VIII reforma 2017...
- Program III etap (2012r.)
- Wzory
- Nauczyciele
- Arkusze maturalne CKE matematyka
- Arkusze maturalne próbne MegaMatma z matematyki
- Wszystkie klasówki (200)
- 1. Liczby wymierne dodatnie
- Ponadpodstawowa
- 1. Liczby rzeczywiste
- 2. Wyrażenia algebraiczne
- 3. Równania i nierówności
- 3.1 Sprawdzanie czy dana liczba ...
- 3.2 Równania kwadratowe z jedną ...
- 3.3 Nierówności kwadratowe z ...
- 3.4 (R)Wzory Viète'a. ...
- 3.5 (R)Nierówności liniowe i ...
- 3.6 Układy równań pierwszego ...
- 3.7 (R)Układy równań ...
- 3.8 Rozwiązywanie równań typu ...
- 3.9 (R)Nierówności wielomianowe....
- 3.10 (R)Reszta z dzielenia ...
- 3.11 (R)Pierwiastki wymierne ...
- 3.12 (R)Rozwiązywanie równań ...
- 3.13 Rozwiązywanie równań ...
- 3.14 (R)Rozwiązywanie ...
- 3.15 (R)Rozwiązywanie równań i ...
- Klasówki (31)
- 4. Funkcje
- 4.1 Sposoby określania funkcji. ...
- 4.2 Obliczanie wartości funkcji ...
- 4.3 Rysowanie wykresów funkcji ...
- 4.3.2 Rysowanie wykresów funkcji ...
- 4.4 (R)Rysowanie wykresów ...
- 4.4.2 (R)Rysowanie wykresów ...
- 4.4.3 (R)Rysowanie wykresów ...
- 4.5 Wykres funkcji liniowej z ...
- 4.6 Wykres funkcji kwadratowej ze ...
- 4.7 Postać kanoniczna, ogólna i ...
- 4.8 Wartość najmniejsza i ...
- 4.9 Zastosowanie funkcji liniowej ...
- 4.10 Wykresy funkcji ...
- 4.11 (R)Wykresy funkcji ...
- 4.12 Zastosowania funkcji ...
- 4.13 (R)Zastosowania funkcji ...
- 4.14 Wykres funkcji f(x)=a/x, ...
- 4.15 (>R)Wykresy funkcji ...
- 4.16 (R)Wykresy funkcji danych ...
- Klasówki (30)
- 5. Ciągi
- 6. Trygonometria
- 6.1 (R)Miara łukowa kąta a ...
- 6.2 Sinus, cosinus i tangens ...
- 6.2.2 Wyznaczanie wartości funkcji ...
- 6.3 (R)Wyznaczanie wartości ...
- 6.4 Zależności między ...
- 6.5 (R)Okresowość funkcji ...
- 6.6 (R)Funkcje trygonometryczne ...
- 6.7 (R)Sinus sumy i cosinus sumy ...
- 6.8 (R)Równania i nierówności ...
- Klasówki (21)
- 7. Planimetria (Geometria na płaszczyźnie)
- 8. Geometria analityczna (Geometria na płaszczyźnie kartezjańskiej)
- 8.1 Równanie prostej ...
- 8.2 (R)Równoległość i ...
- 8.2.2 (R)Równoległość i ...
- 8.3 Punkt przecięcia dwóch ...
- 8.3.2 Punkt przecięcia dwóch ...
- 8.4 (R)Interpretacja graficzna ...
- 8.5 (R)Odległość punktu od ...
- 8.5.2 (R)Odległość punktu od ...
- 8.6 Obrazy figur w symetrii ...
- 8.7 (R)Współrzędne wektora i ...
- 8.7.2 (R)Współrzędne wektora i ...
- 8.8 (R)Przesunięcie wykresu ...
- Klasówki (26)
- 9. Stereometria
- 10. Elementy statystyki opisowej
- 11. Kombinatoryka i teoria prawdopodobieństwa
- 12. Rachunek różniczkowy
- Program IV etap (2012r.)
- Program reforma 2017...
- Wzory
- Nauczyciele
- Arkusze maturalne CKE matematyka
- Arkusze maturalne próbne MegaMatma z matematyki
- Wszystkie klasówki (200)
- Studia
- Wzory matematyczne
- Symbole
- Wiadomości praktyczne
- Wyrażenia algebraiczne
- Logarytmy
- Funkcje
- Trygonometria
- Analiza matematyczna
- Geometria analityczna
- Kombinatoryka
- Rach.prawdopodobieństwa
- Statystyka opisowa
- Planimetria
- Stereometria
- Logika matematyczna
- Algebra zbiorów
- Algebra liniowa
- Tabele
- Wzory do pobrania PDF
- Wzory
- Nauczyciele
- Arkusze maturalne CKE matematyka
- Arkusze maturalne próbne MegaMatma z matematyki
- Wszystkie klasówki (200)
- E-BOOKI MegaMatma
![[close]](/skin/frontend/close.png)









